반응형

라플라스 변환 (Laplace Transform)
라플라스 변환은 공학 및 수학에서 주로 사용되는 적분 변환 중 하나로, 시간 영역(time domain)의 함수를 복소수 영역(s-domain)의 함수로 변환합니다. 이를 통해 미분 방정식의 해를 구하거나 시스템의 동작을 분석하는 데 유용합니다. 라플라스 변환은 제어 이론, 신호 처리, 회로 이론 등 다양한 분야에서 사용됩니다.
라플라스 변환의 정의
라플라스 변환은 함수 를 다음과 같이 변환합니다.


라플라스 변환의 주요 성질
라플라스 변환은 다음과 같은 중요한 성질을 가집니다.
선형성 (Linearity)
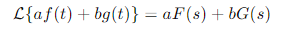
여기서 와 는 상수, 와 는 각각 와 의 라플라스 변환입니다.
시간 이동 (Time Shifting)

여기서 는 단위 계단 함수입니다.
주파수 이동 (Frequency Shifting)

미분 (Differentiation)

적분 (Integration)

역 라플라스 변환 (Inverse Laplace Transform)
라플라스 변환의 역변환은 F(s)F(s)를 다시 시간 영역의 함수 f(t)f(t)로 변환하는 것입니다. 이는 다음과 같이 정의됩니다.

역 라플라스 변환을 구하는 일반적인 방법으로는 부분 분수 분해, 라플라스 변환표, 복소수 적분 등이 있습니다.
예시문제




반응형
'전기' 카테고리의 다른 글
| 라플라스 역변환 (정의,공식,예시문제) (1) | 2024.07.10 |
|---|---|
| 자주 쓰는 라플라스 변환 공식 (0) | 2024.07.10 |
| 무왜형 선로 (회로이론) (0) | 2024.07.10 |
| 무손실 선로 (회로이론) (0) | 2024.07.10 |
| 특성 임피던스와 전파 정수 (0) | 2024.07.10 |



